Jun 16, 2014 That’s what the GTO approach is in the game of chicken, but how does that relate to poker? Take an overly-simplified situation where on the river there’s a $500 pot, we have $500 effective, and we decide to jam the river. We’re going to say that we have the best hand 2/3 of the time and we have total air 1/3 of the time. Essentially, an online poker bot is a computer program that have been designed to play the game against human opponents or other pieces of software on multiple poker rooms. Once activated, out Texas Holdem poker bot will load a formula allowing it to play the game with a view to making profitable long-term decisions.
These days I witness poker players brandishing the phrase “GTO poker” like it's a selfie stick at the beach. Sure, it’s a sexy idea — to apply “optimal theory” to your game — but there’s an essential aspect to the idea that most players miss.

While pure game theory optimal solutions (i.e., equilibria) are characterized by two players playing perfectly, GTO can still be used to analyze spots where your opponent is far from perfect. In fact, since the vast majority of us are imperfect (a.k.a. human) players, arguably the real power of GTO analysis is how it can improve your exploitative play.
To understand this, let’s walk through the typical steps of GTO analysis.
Step 1 - Pick a Hand, Any Hand
For this exercise, you’ll need a poker hand. You can make one up, or, even better, pick one you’ve played recently. I suggest selecting a spot where you were wondering what to do on either the turn or the river. All of the solvers mentioned below are free to use if you’re analyzing later streets, but they cost money if your analysis begins on the flop (or earlier).
Take note of the positions and any reads you have on your opponent as this will help you assign hand ranges more realistically.
Step 2 - Choose your Solver
Why do math by hand when you can use a calculator?
GTO calculators are called “solvers,” and there are three main ones on the market:
- GTO Range Builder - More graphical/visual. Web version only. Lots of educational material.
- SimplePostflop - More tabular. Standalone version. Can start the analysis preflop.
- PioSOLVER - More tabular. Standalone version. Preferred by high stakes players.
You might consider starting with GTO Range Builder, since it has a web interface and is the fastest and simplest to try. A in-depth comparison of solvers can be found in this post and responses on Two Plus Two. And for specifics on how to use each of the solvers, refer to their tutorials.
Step 3 - Enter the Hand Ranges
With a hand in mind and a solver in hand, it’s time to enter the data. Any good analysis starts with assigning hand ranges.
Stop and consider which hands your opponent might be holding given the action so far. Enter them into the solver. Which hands could you possibly be holding in this spot? Enter those as well.
Step 4 - Find the GTO Solution
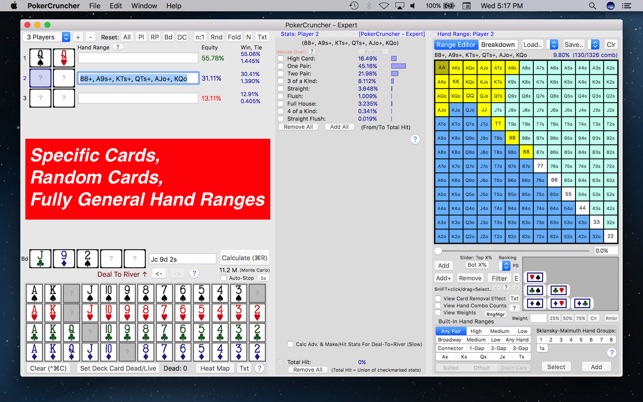
Next enter the other facts about the hand such as board cards, pot size, effective stacks and what kind of bet sizes you think will be used. Then run the solver.
If you’re analyzing the turn or river, this should only take a few seconds. Flop analysis can take a few minutes or up to an hour depending on the solver and the hardware used to run it.
The output will be your GTO solution. The solution specifies what each player should do with every hand in his range. Now you can look up the specific hand you were holding and take note of how you would play it if you were both playing perfectly.
Step 5 - Find the Exploitable Solution
Now comes the critical step.
Since obviously no one is playing perfectly, we want to determine our optimal real world solution. Each tool has a feature where you can manually change the solution to reflect what you think your opponent is most likely to do. This is called “locking” your opponent’s strategy.
Perhaps the tool says a perfect opponent should always check to you on the river, but you know this guy will bet his top-pair hands and better. You can lock that strategy into the tool, and then recalculate the solution.
You now have an exploitative recommendation that will yield the maximum possible value based on how your opponent actually plays!
If you’re not sure how your opponent plays, perhaps because he’s unknown to you, then you can simply default to the solver’s GTO solution.
Seize the Opportunity
This is a powerful technique. You are taking much of the guesswork out of estimating how to exploit your opponent. And the results can sometimes be surprising and often enlightening.
Also, this kind of analysis is relatively new. The solvers themselves have appeared in only the last couple years. Perusing the web (try googling “Poker GTO”), the amount of instructional material available on these concepts is slim but growing fast.
An opportunity therefore exists for the more ambitious students of the game. Soon perhaps these tools will get integrated into the popular database programs like Hold’em Manager and Poker Tracker, but until then I suggest you spend some time with these tools and techniques and increase your edge over the competition.

Mike Gano is a professional poker player, coach, streamer, and author. He’s been a consistent winner for over a decade in the online cash games, currently playing 200NL on 888poker. He’s created educational videos for CardRunners, DeucesCracked, Red Chip Poker, and Hold’em Manager. Check out his weekly poker strategy blog called Poker in a Box.
Want to stay atop all the latest in the poker world? If so, make sure to get PokerNews updates on your social media outlets. Follow us on Twitter and find us on both Facebook and Google+!
Tags
cash game strategytournament strategygame theory optimalGTOonline pokertoolssoftware
The famous mathematician John Nash died in a car crash last month, along with his wife, Alicia. They were on their way home from Norway, where Mr. Nash had received the prestigious Abel Prize for his contributions to mathematics. He had previously won the 1994 Nobel Prize in economics. Many people outside of academic circles knew of Nash only through his biography, A Beautiful Mind, and the 2001 film of the same name.
What do Nash and his contributions have to do with poker? Plenty. You may have heard people talk about an “unexploitable” poker strategy. That concept stems from Nash’s work. In order to explain the connection, it helps to start with a game far less complicated than poker, something called “The Prisoner’s Dilemma.”
The Prisoner’s Dilemma
Here’s how it works, as spelled out by another mathematician, Albert W. Tucker, whose explanation appears in the Wikipedia entry on the game:
Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The prosecutors do not have enough evidence to convict the pair on the principal charge. They hope to get both sentenced to a year in prison on a lesser charge. Simultaneously, the prosecutors offer each prisoner a bargain. Each prisoner is given the opportunity either to betray the other by testifying that the other committed the crime, or to cooperate with the other by remaining silent. Here is the offer:
- If A and B each betray the other, each of them serves 2 years in prison
- If A betrays B but B remains silent, A will be set free and B will serve 3 years in prison (and vice-versa)
- If A and B both remain silent, both of them will only serve 1 year in prison (on the lesser charge)
The choice to remain silent can also be called “cooperating,” while betrayal can also be called “defecting.”
Suppose you’re A. What should you do? It obviously depends on what B will choose. If B betrays you, then you’ll either serve 2 years if you also betray, or you’ll serve 3 years if you remain silent. Clearly, then, if B chooses to betray, you’re better off also betraying.
What if B remains silent? Then you’ll either serve 1 year by also remaining silent, or go free by betraying B. So if B remains silent, you’re better off betraying him.
Therefore, betrayal is your best choice regardless of what B chooses to do. And, symmetrically, B’s analysis of his best choice comes out the same way. This is a simple example of what’s called a “Nash equilibrium.”
Note that the key factor is not that both players in this game get their best possible outcome. They don’t; neither one goes free, or even gets the reduced sentence of just one year in prison. The key thing that makes this a Nash equilibrium is that each has chosen a strategy in which his outcome cannot be made worse by any choice made by the other participant.
Game Theory Optimal (GTO) Strategy
The concept of an unexploitable strategy in poker derives directly from this. It refers to a decision in some particular situation for which an opponent cannot make a profitable counter. Another term for such a strategy is “game theory optimal” or GTO.
For every decision you have to make in poker, there is a GTO solution. For most situations, what that solution is usually cannot be known, because poker is such a complex game that even the best computers running the best algorithms cannot calculate it. But an optimal decision does exist. If you were to make every poker decision according to this theoretical model, then no strategy that an opponent could choose would make you a long-term loser.
Of course, nobody plays that way. Real-world human players deviate from GTO all the time, which is what opens them up to being exploited.
To use an absurdly exaggerated example, if you had an opponent in heads-up hold’em who was so tight that he played only when he had pocket aces, and you knew this, you could rob him blind. If he ever voluntarily put money into the pot, then you would know he had aces, and you would fold. Otherwise, you raise, he folds, you take the pot. On average, he would win once every 221 hands, and you would win all the rest.
Raising every hand in this very specific situation would be hugely profitable, because it exploits a terrible flaw — pathological tightness — in your opponent’s play. Doing so requires you to deviate from GTO play yourself, as clearly raising every hand is not generally a profitable long-term strategy.
The deviation that you make from GTO play in turn makes you exploitable. If we introduce a third player into the game who has observed the heads-up dynamics, you obviously can’t continue to raise every hand, because the third player can now take advantage of your excessively aggressive play by selectively reraising you, and you’ll be forced to fold at least your weakest hands.
Gto In Poker
Applications to Poker
Are there real-world poker situations where the idea of the Nash equilibrium strategy applies that aren’t as contrived as these examples? Yes, there are.
You may have seen tables of “push-or-fold” strategies. These are for short-handed or heads-up tournament play with relatively short stacks, such that the only two rational choices are to fold or go all in, nothing in between. Because the situation is a simple one, it has been possible to work out mathematically which hands you should fold and which you should shove, such that your decision is unexploitable — that is, your opponent cannot adopt any strategy that improves his own outcome at your expense.
In January of this year, a team at the University of Alberta announced a computer algorithm that plays GTO poker, though only in the specific situation of heads-up, fixed-limit Texas hold’em. The best that any opponent can hope to do against this bot in the long run is break even.
However, as many commentators were quick to point out, that does not mean that the software would do particularly well against any given opponent compared to what an expert human player could do. That’s because the computer’s fixed strategy — it has predetermined what to do in every possible situation — cannot deviate from GTO to exploit the mistakes made by a flawed opponent.
Put another way, a fishy player will certainly lose all his money to the computer over time. But a wily shark of a human opponent will take the fish’s money even faster, because he can analyze the fish’s mistakes and adjust his play to take advantage of the weaker player.
In our original example, neither prisoner’s choice can be exploited advantageously by the other. But neither ends up with his optimal outcome, which would be to go free. Similarly, the perfect GTO-playing computer cannot be beaten, but it also fails to maximize its profits by spotting and exploiting the inevitable errors of its opponents. GTO play is essentially a defensive strategy, not the maximally profitable one.
Gto Poker Pdf
Real-world poker never involves opponents who are playing a GTO strategy. Every player makes frequent mistakes. The profit in the game is in being better at identifying and exploiting their mistakes than they are at identifying and exploiting yours.
Conclusion
To return to honoring the man whose work inspired this article, if your opponents aren’t playing Nash-equilibrium poker — and they never are — then you shouldn’t either. Find their weaknesses and make them pay for them while being careful not to let your own play deviate so far from the theoretical optimum that you become easy to exploit.
It is likely to be many years before a game as complex as full-ring, deep-stack, no-limit hold’em is fully “solved,” meaning that the GTO move for every possible situation has been determined. When that day comes, however, remember to tip your poker eyeshade to John Nash, whose beautiful mind will have been what made it possible.
Lower photo: “John Forbes Nash, Jr.,” Peter Badge. Creative Commons Attribution-ShareAlike 3.0 Unported.
Robert Woolley lives in Asheville, NC. He spent several years in Las Vegas and chronicled his life in poker on the “Poker Grump” blog.
Want to stay atop all the latest in the poker world? If so, make sure to get PokerNews updates on your social media outlets. Follow us on Twitter and find us on both Facebook and Google+!
Gto Poker Guide
Tags
cash game strategytournament strategygame theorygame theory optimal poker strategyJohn NashA Beautiful Mindmathematicspoker math